KD-Tree
KD树
KD树 KD-Tree(k-dimensional tree的简称), 可以实现k近邻搜索, 构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分 k-d树每个结点都是k维的点二叉树, 所有非叶子节点可以看作用超平面把空间分成两个部分, 节点左子树代表超平面左边的点, 右子树代表右边的点
适合需要进行相邻区间和查询的情况, 比如需要找到一个点附近的一些点, 维护这些点之间的状态, 就可以用八叉树 适用KD树的情况:数据量大,且点位更新不频繁
适合需要进行相邻区间和查询的情况, 比如需要找到一个点附近的一些点, 维护这些点之间的状态, 就可以用八叉树 适用KD树的情况:数据量大,且点位更新不频繁
建树
建树流程: 取任意维度, 然后取该维度中位点, 由该点按该维度将树划分成左右两部分, 对划分后的部分依次重复次操作,直到划分后没有子树 如以下6个点:(5,4) (2,3) (9,6) (7,2) (8,1) (4,7) , 建树结果如下:
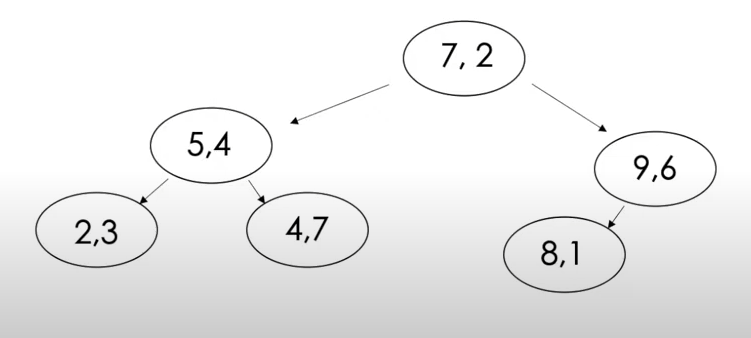
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public class KDTreeNode
{
public KDTreeNode lchild;
public KDTreeNode rchild;
public Vector2 pos;
public KDTreeNode(Vector2 position)
{
pos = position;
}
}
public class CompareVector : IComparer<Vector2>
{
int m_dimension;
public CompareVector(int dimension)
{
m_dimension = dimension;
}
public int Compare(Vector2 x, Vector2 y)
{
return x[m_dimension].CompareTo(y[m_dimension]);
}
}
public class KDTree
{
//KD树根节点
public KDTreeNode rootNode;
public KDTree(Vector2[] nodes)
{
int dimension = 0;
rootNode = BuildTree(nodes, 0, nodes.Length, dimension);
PrintTree(rootNode);
}
KDTreeNode BuildTree(Vector2[] nodes, int index, int length, int dimension)
{
if (length <= 0)
{
return null;
}
if (length == 1)
{
return new KDTreeNode(nodes[index]);
}
Array.Sort(nodes, index, length, new CompareVector(dimension));
//在数量为偶数时,取中点有不同取法, 这里选择数值较大点
int midIndex = index + length / 2;// - (length % 2 == 0 && dimension == 0 ? 1 : 0);
KDTreeNode tep;
tep = new KDTreeNode(nodes[midIndex]);
tep.lchild = BuildTree(nodes, index, midIndex - index, (dimension + 1) % 2);
tep.rchild = BuildTree(nodes, midIndex + 1, length - (midIndex - index + 1), (dimension + 1) % 2);
return tep;
}
}
本文由作者按照 CC BY 4.0 进行授权